BAB II (Persamaan Garis, Gradien dan Sudut Inklinasi)

A. Persamaan  Garis, Gradien dan Sudut Inklinasi

1. Persamaan Umum Garis

      Garis dibentuk oleh paling sedikit dua buah titik berbeda. Sebagai suatu himpunan, garis merupakan himpunan titik-titik yang tak hingga dan tak berbatas sehingga garis tidak memiliki dimensi panjang. Garis juga merupakan titik-titik yang bergerak scara kontinu.

     

Jika garis dibentuk oleh titik A dan B maka garis tersebut dapat dinamakan sebagai garis AB.

       Notasi lain untuk penamaan garis yaitu menggunakan huruf kecil misalnya g, h, l, m dan sebagainya.

        Sebuah garis juga disebut kurva berderajat satu yang dinyatakan sebagai :

Ax + By + C = 0 untuk A, B, C bilangan riil dan x, y variabel bilangan riil

       Sebuah garis dapat ditentukan persamaan kurva berderajat satu seperti di atas apabila diketahui tiga buah titik yang dilalui oleh garis tersebut.

Contoh :
Sebuah garis yang melalui titik A(1,2) B (-3,4) C(5,0) maka persamaan kurva berderajat satu untuk garis tersebut ditentukann sebagai berikut :

Cara 1 : Ax+By+C=0
Langkah 1 
Substitusikan Koordinat titik ke dalam persamaan titik

A(1,2)  ➡ A + 2B + C = 0 .............(1)
B(-3,4) ➡ -3A+4B+ C = 0 .............(2)
C(5,0)  ➡ 5 A + C = 0..................(3)

Langkah 2
Menyelesaikan sistem Persamaan Linear

A + 2B + C = 0
-3A+4B + C = 0   
4A - 2 B     = 0
            B   = 2A

misalkan A=1 dan B =2,

Kita masukkan ke persamaan A + 2B +2C = 0, maka didapatkan bahwa C =-5
Cek Kebenaran A =1 , B = 2 dan C = -5 ke Pers-1,pers-2, dan pers-3. ama hasilnay sama

Langkah 3
Menjadikan ke persamaan kurva berderajat satu

Ax + By + C = 0
x + 2y -5 =0




Cara 2 : y = mx + c
Substitusikan Koordinat titik ke dalam persamaan titik

A(1,2)  ➡ 2= m + c...................(1)
B(-3,4) ➡ 4= -3m + c .................(2)

C(5,0)  ➡ 0 = 5m + c ; c= -5m.......(3)

Substitusikan (3) ke (1)
2 = m - 5m
2 = -4m
m= -1/2 ........(4)

Substitusikan (4) ke (3)
c = -5(-1/2)
c = 5/2

Jadi Persamaan garisnya adalah y= -1/2x + 5/2


2. Gradien dan Sudut Inklinasi

Diketahui sebuah garis dengan persamaan x + 2y -5 =0 . Besarnya sudut yang terbentuk akan mempengaruhi kemiringan garis. Kemiringingan suatu garis tersebut dinamakan gradien (m). Sedangkan suatu sudut yang bernilai positif dan dibentuk antara garis dan sumbu x positif disebut sudut inklinasi (∝).

Nilai gradien suatu garis dapat bernilai positif, negatif, nol atau tidak terdefinisi. Untuk mencari suatu gradien dari sebuah garis dapat menggunakan rumus.

Jadi nilai gradien suatu garis merupakan nilai tangen sudut inklinasi dan besarnya sudut inklanasi adalah nilai arc tan dari gradien garis.

Dari persamaan garis x + 2y -5 dapat dicari nilai gradiennya yaitu :

2y = 5-x

y = 5/2 –x/2

dari persamaan y = mx +c , jadi nilai gradiennya adalah -1/2. Dengan sudut inklinasinya adalah arc tan -1/2 = 153,43^o.

Hubungan Sudut Inklinasi dan Gradien

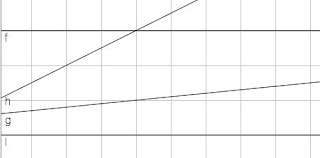
Deskripsikan bentuk masing-masing garis berdasarkan gradien dan sudut inklinasi yang ditunjukkan pada gambar berikut.

Diketahui : Empat garis berbeda p = AB, q = AC, r = BC, dan s = BD

Ditanyakan : Bentuk garis p, q, r dan s berdasarkan gradien dan sudut inklinasi … ?

Penyelesaian :

Mencari Gradien dengan Menggunakan Rumus 

 

p = AB ---> m = 3/4

q = AC ---> m = 0

r  = BC ---> m = -3/2

s  = BD ---> m = tidak terdefinisi

sudut inklinasi = Arc tan dari Gradien

Gradien = Arc tan dari sudut inklinasi

Mencair Sudut inklinasi  :

garis p , ∝ = arc tan (3/4) = 36,87

garis q,  ∝ = arc tan 0 = 0

garis r,  ∝ = arc tan (-3/2) = 123,69

garis s,  ∝ = arc tan ∞ = 90

Persamaan garis yang melalui  2 titik

garis p = A(1,1) dan B(5,4)

y-y1 =m(x-x1)
y-1   = 3/4 (x-1)
4y-4 = 3x-3
   4y = 3 x + 1

    y  = 3/4x +1/4

garis q = A(1,1) dan C(7,1)

y-y1  =m(x-x1)
y-1    = 0 (x-1)
      y =  1

garis r =  B(5,4) dan C (7,1)

y-y1 =m(x-x1)
y-4   = -3/2 (x-1)
2y-8 = -3x + 15
   2y = 23-3x

    y  = -3/2x +23/2

garis s = B(5,4) dan D(5,1)

y-y1  =m(x-x1)
karena tidak terdefinisi maka x=5

TABEL HUBUNGAN ANTARA GRADIEN, SUDUT INKLINASI DAN BENTUK GARIS

Garis	Persamaan garis	Nilai gradien	Nilai sudut inklinasi	Deskripsi bentuk garis
p	y=3/4x +1/4	m>0	Sudut lancip	Dari kiri bawah ke kanan atas
q	y=1	m=0	0	Mendatar, sejajar sb-x
r	y=-3/2x+23/2	m<0	Sudut tumpul	Dari kiri atas ke kanan bawah
s	x=5	m tidak  terdefinisi	90	Horizontal sejajar sb-y

Referensi:

Sukirman. 1993. Geometri Analitik Bidang dan Ruang. Jakarta: Departemen Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Dasar dan Menengah.

Catatan Kuliah Geometri Analitik 

Dosen Pengampu : Della Maulidiya, S.Si., M.Kom dan Nur Aliyyah Irsal, M.Pd.