BAB IV (Persamaan Kutub)

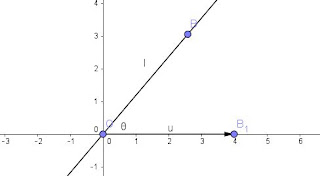
Grafik garis lurus yang melalui titik asal dan membentuk sudut θ dengan sumbu kutub.

Perhatikan gambar dibawah ini  yaitu garis lurus m yang berjarak d dari kutub (d>0) dann θ adalah sudut antara sumbu kutub dan garis yang tegak lurus dari kutub pada garis m. tentukan persamaan kutub untuk garis m

kita ambil sembarang titik P(r,θ) pada garis m. Pada segitiga OTP dengan <POT = θ-θo
 berlaku

cos (θ-θo) = d/r
r = d / cos (θ-θo)

Karena P (r, θ) sebarang titik pada garis m dan berlaku hubungan tersebut, maka untuk setiap titik pada garis m berlaku hubungan itu.

Jadi persamaan kutub untuk garis lurus yang berjarak d dari kutub dan normalnya membrntuk sudut θo dengann sumbu kutub adalah

r = d / cos ( θ - θo)

Persamaan fungsi diubah menjadi persamaan kutub :

Grafik dan Persamaan Kutub :

a. Limason dan Kardioda

     r = a ± b cos θ , r = a ± b sin θ

    dengan a,b konstanta yang positif

    Grafiknya disebt limason, apabila a=b grafiknya dinamakan kardioda

    

 b. Lemniskat

     r²= ± a cos 2θ,  r²= ± a sin 2θ

     dengan a suatu konstanta positif

c. Mawar

    r=  a cos nθ , r=  a sin nθ

    dengan a suatu konstanta

d. Spiral

     r = aθ

     dengan a konstanta

Referensi:

Sukirman. 1993. Geometri Analitik Bidang dan Ruang. Jakarta: Departemen Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Dasar dan Menengah.

Catatan Kuliah Geometri Analitik 

Dosen Pengampu : Della Maulidiya, S.Si., M.Kom dan Nur Aliyyah Irsal, M.Pd.