Dalam sistem koordinat kartesius ini kita ambil patokan bahwa sumbu y diambil mendatar (arah kanan (+) dan arah kiri (-)), sumbu z diambil vertikal (arah atas (+) dan arah bawah (-) sedangkan sumbu x yang menuju arah kita sebagai arah positif dan arah lawannya adalah negatif.
ketiga sumbu tersebut menentukan tiga bidang, yaitu bidang xy, bidang xz dan bidang yz. Ketiga bidang ini membagi ruang menjadi delapan oktan, yaitu oktan I,II,II,IV,...,VIII.
Oktan I,II,III,IV diatas bidang xy
Oktan V,VI,VII,VIII dibawah bidang xy
Oktan I : (x+ , y+, z+)
Oktan II : (x+ , y-, z+)
Oktan III : (x- , y-, z+)
Oktan IV : (x- , y+, z+)
O ktan V : (x+ , y+, z-)
Oktan VI : (x+ , y-, z-)
Oktan VII : (x- , y-, z-)
Oktan VIII : (x- , y+, z-)
Cara membuat suatu titik P(x,y,z)
1. proyeksi bidang xy, z = 0
A(x,y,0)
2. proyeksi bidang xz, y = 0
B(x,0,z)
3. proyeksi bidang yz, x = 0
C(0,y,z)
contoh menggambarkan titik
Cara lain menggambarkan titik P(x,y,z)
1. Letakkan titik di koordinat x
2. Geser ke kanak atau ke kiri sesuai dengan titik yanng ditentukan
3. Geser ke atas atau ke bawah sesuai dengan titik yang ditentukan.
Contoh gambar
Jarak antar Titik
Untuk mengetahui jarak antar dua titik tersebut didapatkan dengan cara.
1. Gambarkan proyeksi titik P dan R sehingga didapatkan 2 balok
2. Dari titik P dan R dibuat balok sedemikian hingga titik P dan R tersebut adalah diagonal ruang balok tersebut.
3. Kemudian Proyeksikan titik P ke bidang XY sehingga didapatkan PR
4. segitiga PQR membentuk sebuah segitiga siku siku
5. Dengan menggunakan rumus Phytagoras maka didapatkan bahwa panjang PQ adalah :
Vektor dalam Ruang Dimensi Tiga
Dalam
ruang-ruang dimensi tiga suatu titik dinyatakan dengan tiga komponen, yaitu
absis, ordinat dan aplikat. Misalnya B(x1, y1, z1). Vektor posisi (terhadap titik O) untuk titik B
adalah a = < x1, y1, z1> = x1i, y1j, z1k.
Vektor-vektor
basis i,j,k berturut-turut adalah vektor-vektor satuan yang
searah dengan sumbu-sumbu x positif, y positif dan z positif.
Semua sifat
penjumlahan vekotr dan perkalian vekotr dengan skalar yang berlaku dalam bidang
datar juga berlaku untuk vektor dalam ruang dimensi tiga.
PANJANG VEKTOR
Jika a =
< x1, y1, z1> maka panjang vektor a adalah,
PERKALIAN TITIK
PADA VEKTOR
Jika u =
< u1, u2, u3> dan v = < v1, v2, v3>, maka perkalian titiknya didefinisikan sebagai
berikut
Dengan θ adalah
sudut yang dibentuk oleh u dan v dan serta 0
≤ θ ≤ phi
Dari definisi
diatass didaptkan rumus sudut yang dibentuk oleh vektor u dan v yaitu,
PERKALIAN
VEKTOR
Jika u =
< u1, u2, u3> dan v = < v1, v2, v3> maka perkalian kedua vektor adalah,
HASIL KALI
SILANG DUA VEKTOR
Perkalian
silang dua vektor a = a1i + a2j + a3k dan b = b1i + b2j + b3k didefinisikan sebagai berikut,
Dengan θ adalah
sudut yang dibentuk kedua vektor dan u adalah vektor satun
yang tegak lurus pada a dan b.
Referensi:
Sukirman. 1993. Geometri Analitik Bidang dan Ruang. Jakarta: Departemen Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Dasar dan Menengah.
Catatan Kuliah Geometri Analitik
Dosen Pengampu : Della Maulidiya, S.Si., M.Kom dan Nur Aliyyah Irsal, M.Pd.









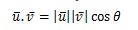



Komentar
Posting Komentar